U.S. Department of Health and Human Services
The Effects of Sample Attrition on Estimates of Channelings Impacts for an Early Sample
Peter A. Mossel and Randall S. Brown
Mathematica Policy Research, Inc.
July 1984
The paper was written as part of contract #HHS-100-80-0157 between ASPE and Mathematica Policy Research, Inc., and contract #HHS-100-80-0133 between ASPE and Temple University. Additional funding was provided by the Administration on Aging and Health Care Financing Administration (now CMS). For additional information about this subject, you can visit the DALTCP home page at http://aspe.hhs.gov/_/office_specific/daltcp.cfm or contact the office at HHS/ASPE/DALTCP, Room 424E, H.H. Humphrey Building, 200 Independence Avenue, S.W., Washington, D.C. 20201. The e-mail address is: webmaster.DALTCP@hhs.gov. The Project Officer was Robert Clark.
This report was prepared for the Department of Health and Human Services under contract no. HHS-100-80-0157. The DHHS project officer is Ms. Mary Harahan, Office of the Secretary, Department of Health and Human Services, Room 4477F, Hubert H. Humphrey Building, Washington, DC. 20201.
TABLE OF CONTENTS
- I. INTRODUCTION
- VI. CONCLUSION
- APPENDIX A: A MULTINOMIAL LOGIT MODEL OF RESPONSE, DEATH, AND NONRESPONSE
- APPENDIX B: COMPARISON OF RESULTS TO THOSE PRESENTED IN CHANNELING EFFECTS FOR AN EARLY SAMPLE AT 6-MONTH FOLLOWUP
- LIST OF TABLES
- TABLE 1: Attrition Rates for the Preliminary Impact Analysis Samples and Reasons for Attrition
- TABLE 2: Probit Coefficients for Being in the Known Status Sample or the Followup Sample
- TABLE 3: Estimates of Impacts of Channeling With and Without Adjustment for Attrition
- TABLE A-1: Multinomial Logit Coefficients for Response Status at Six-Month Followup
- TABLE B-1: Comparison of Impact Estimates in Preliminary Analysis Report to Unadjusted Impact Estimates Used in Attrition Analysis
ACKNOWLEDGMENTS
Several individuals besides the authors contributed to the production of this report. Peter Kemper, George Carcagno, and Judith Wooldridge provided valuable advice and comments on an early draft of this report. Daniel Buckley and Shari Miller Dunstan provided able computational assistance. Felicity Skidmore provided valuable editorial guidance. Daniel Steinberg provided us with prerelease versions of probit and multinomial logit programs. Annette Kasprack performed the necessary word processing for this report.
PREFACE
This report serves as a supplement to the report "Channeling Effects for an Early Sample at 6-Month Followup" (Kemper et al., 1984). That report examined overall channeling impacts on a variety of outcome measures from 6-month followup interviews with channeling treatment and control group members (or proxy respondents). This report is based on data from the same source for the same sample of early participants in the National Long Term Care Demonstration. In this report we assume that the reader is familiar with the channeling demonstration, research methodology, and impact estimates described in the main report. We limit our discussion in this report to how impact estimates for a subset of the outcome variables examined there are affected by sample attrition.
I. INTRODUCTION
In the channeling evaluation, as in other longitudinal studies, we are faced with the fact that some of the members of the research sample are lost to the analysis due to attrition.1 In an earlier report (Brown and Harrigan, 1983) we showed that the treatment and control groups at the time of randomization comprised similar types of individuals; hence, post-randomization differences between those two groups can be attributed to the effects of channeling. However, sample attrition may distort the treatment/control comparison, depending on the type of attrition that takes place. Attrition that is completely random with respect to all factors relevant to the outcome being measured leads to less precise estimates of program impacts (due to the reduction of the sample size), but does not lead to biased estimates. However, if the pattern of attrition is different for the treatment and control groups, the sample of treatment and control group members available for analysis will no longer be similar. In this case, differences in outcomes between the groups cannot be attributed to channeling alone, and impact estimates that do not adjust for the initial differences induced by different attrition patterns will be biased.
The purpose of this report is to investigate whether there is evidence of bias due to attrition in the preliminary estimates of channeling's impacts, which are based on observations six months after randomization, and which are presented in Kemper et al. (1984). Section II describes the pattern of attrition. Section III discusses how bias due to attrition might arise in the impact estimates. Section IV outlines the statistical procedures used to correct for bias, and Section V contains the results obtained when this procedure is used to estimate the impacts of channeling for key outcome measures drawn from the preliminary findings. Finally, we draw some conclusions about the extent of attrition bias in the preliminary impact estimates and discuss the implications of these results for dealing with the problem of potential attrition bias in the final report.
II. THE NATURE AND EXTENT OF ATTRITION IN THE PRELIMINARY ANALYSIS SAMPLE
In the preliminary report, the impact of channeling is estimated on a sample consisting of the early enrollees only--those who applied to channeling and were randomly assigned to the treatment or control group on or prior to January 31, 1983. Two different subsets of this early cohort were used in the analysis.
The known status sample consists of those sample members who completed the baseline and for whom status (whether the sample member was dead, in a nursing. home, in a hospital, or living in the community) at the point six months after randomization is known. Attrition from this sample is defined as either nonresponse to the baseline interview or missing data on status at six months. The known status sample was used to estimate channeling's impact on all outcome measures that could be determined from knowledge that the sample member was dead or in a nursing home or hospital six months after the day on which he/she was randomly assigned to the treatment or control group, even if no followup were completed. These outcomes included mortality, type of residence, receipt of formal community-based services, and receipt of informal care.
The followup sample consists of the known status sample members for whom a 6-month followup interview was available. Attrition from this sample is defined as nonresponse to the followup interview.2 The followup sample is used to estimate channeling's impact on hospital and nursing home use during the six months preceding the followup interview, receipt of case management during this period, and sample members' well-being at followup.
A sample member can also be omitted from the analysis of impacts on a given outcome measure due to item nonresponse on the outcome variable. In general, there is little item nonresponse for the outcome variables examined in Kemper et al. (1984), and it is not considered to be likely to cause attrition bias. Thus, the possible effect of item nonresponse on impact estimates is ignored in this analysis.
Table 1 gives a frequency distribution of sample members in the followup sample and the known status sample, by model and treatment status. For the known status sample we find an attrition rate of 19 percent in the basic case management sites, of which 11 percent occurred at the baseline. The financial control sites have an almost identical rate of attrition. For the followup sample we find that in the basic case management sites 36 percent of the sample members are lost due to attrition, 11 percent of which occurred at the baseline as before, since baseline response is a necessary condition for inclusion in both samples. The corresponding rate of attrition for the financial control sites is 35 percent, about the same as for the basic sites.
| TABLE 1. Attrition Rates for the Preliminary Impact Analysis Samples and Reasons for Attrition(percent of total early cohort) | ||||||
| Basic Case Management Model | Financial Control Model | |||||
| Treatment | Control | Total | Treatment | Control | Total | |
| KNOWN STATUS SAMPLE | ||||||
| In Known Status Sample | 83.0 | 77.6 | 80.7 | 87.3 | 70.3 | 80.5 |
| Not in Known Status Sample by Reason for Attrition: | ||||||
| Baseline Nonresponse | ||||||
| Deceased | 2.3 | 3.1 | 2.7 | 1.5 | 2.2 | 1.8 |
| Refused interview | 2.5 | 9.6 | 5.6 | 1.2 | 11.7 | 5.5 |
| Moved or unable to locate | 0.5 | 0.4 | 0.5 | 0.1 | 0.7 | 0.3 |
| Othera | 3.2 | 2.0 | 2.7 | 2.7 | 3.8 | 3.1 |
| Total | 8.7 | 15.0 | 11.4 | 5.5 | 18.5 | 10.7 |
| Baseline Complete, but No Status Information | ||||||
| Refused interview | 3.5 | 2.4 | 3.0 | 1.6 | 4.0 | 2.5 |
| Moved or unable to locate | 1.2 | 0.7 | 1.0 | 1.1 | 2.9 | 1.9 |
| Othera | 3.6 | 4.3 | 3.9 | 4.5 | 4.4 | 4.4 |
| Total | 8.3 | 7.3 | 7.9 | 7.3 | 11.2 | 8.8 |
| Total Attrition | 17.0 | 22.4 | 19.3 | 12.7 | 29.7 | 19.5 |
| Total Early Cohort | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| FOLLOWUP SAMPLE | ||||||
| In Followup Sample | 65.0 | 62.5 | 63.9 | 70.7 | 56.5 | 65.0 |
| Not in Followup Sample by Reason for Attrition: | ||||||
| Baseline Nonresponse | ||||||
| Deceased | 2.3 | 3.1 | 2.7 | 1.5 | 2.2 | 1.8 |
| Refused interview | 2.5 | 9.6 | 5.6 | 1.2 | 11.7 | 5.5 |
| Moved or unable to locate | 0.5 | 0.4 | 0.5 | 0.1 | 0.7 | 0.3 |
| Othera | 3.2 | 2.0 | 2.7 | 2.7 | 3.8 | 3.1 |
| Total | 8.7 | 15.0 | 11.4 | 5.5 | 18.5 | 10.7 |
| Baseline Complete, but No Completed Followup | ||||||
| Deceased | 4.3 | 12.1 | 13.4 | 14.4 | 11.2 | 13.1 |
| Refused interview | 5.3 | 4.0 | 4.8 | 2.3 | 5.9 | 3.8 |
| Moved or unable to locate | 2.0 | 1.5 | 1.8 | 1.6 | 3.2 | 2.2 |
| Othera | 4.7 | 4.9 | 4.8 | 5.5 | 4.7 | 5.2 |
| Total | 26.3 | 22.5 | 24.7 | 23.8 | 25.1 | 24.3 |
| Total Attrition | 35.0 | 37.5 | 36.1 | 29.3 | 43.5 | 35.0 |
| Total Early Cohort | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Number of sample members in early cohort | 1,109 | 845 | 1,945 | 1,131 | 758 | 1,889 |
| Number of sample members in known status analysis sample | 921 | 656 | 1,577 | 987 | 533 | 1,520 |
| Number of sample members in followup analysis sample | 721 | 528 | 1,249 | 800 | 428 | 1,228 |
|
||||||
Of more concern than the percentage of the early cohort lost due to attrition is the fact that treatment and control group members differ considerably in overall response rate and in reason for nonresponse. In basic sites, 22.4 percent of controls but only 17 percent of the treatment group are unavailable for the known status analysis sample. The difference between treatment and control groups in attrition rates in the financial control sites is even greater (29.7 percent for controls, 12.7 percent for treatments). The bulk of these treatment/control differences in response rates are due to the difference in refusal rates at baseline. In the basic case management model, 9.6 percent of the control group refused to be interviewed at the baseline, but only 2.5 percent of the treatment group refused. The corresponding figures for the financial control model show an even greater difference, with refusal rates of 11.7 and 1.2 percent for treatment and control groups, respectively.3 Most of the refusals in the control group were proxies or sample members who said they didn't want to be bothered or were too busy or too ill. A smaller fraction of those who refused indicated that they were upset at being assigned to the control group.
Between the baseline and followup interviews the differences between treatment and control group members in rates of attrition persist, although these differences are not as pronounced as at baseline. Thus, it appears that most of the overall treatment/control differences in response rates are caused by differences in baseline nonresponse between these groups. The differential response rates of treatment and control group members raise a concern about potential attrition bias in the impact estimates.
III. HOW ATTRITION MIGHT AFFECT ESTIMATES OF CHANNELING IMPACTS
As noted above, it has been established that as a result of randomization, the full treatment and control groups were composed of similar types of individuals. However, the loss of sample members through attrition can lead to the following situations:
- Different rates of attrition between treatment and control groups, although despite this differential attrition both groups are, on the average, still composed of the same types of individuals as is the full sample, and are therefore similar to each other.
- Different rates of attrition between treatment and control groups, although both groups are still similar to each other. However, due to attrition, the analysis sample is dissimilar to the full sample.
- The treatment and control groups, which were equivalent for the full sample, consist after attrition of different types of individuals.
In the first situation there will be no danger of attrition bias in the impact estimates. However, due to the smaller sample sizes the impact estimates will have a greater variance as compared to those obtained for the full sample. In the second situation, there will be no attrition bias but the results of the demonstration apply only to the analysis sample, rather than to the population that applied and was found eligible for channeling. In the third situation an estimated treatment/control group difference may be caused by the fact that these groups are made up of very different individuals, rather than by the impact of channeling. An example will illustrate this point.
Suppose that we estimate the impact of channeling on the number of hospital days by comparing treatment and control group means, and find that these means are identical at the 6-month followup. Suppose further that the control group available for analysis were to consist of relatively unimpaired individuals, because the more impaired sample members refused further cooperation after learning that they would not receive channeling services. As a consequence, the control group would have had a higher average number of hospital days, had these people remained in the study, and the difference between treatment and control group means would then have been negative. The problem faced here is that an unmeasured variable (impairment) is both of substantial importance in determining the outcome (hospital use) and a cause of sample attrition.
If a good measure of "impairment" were available, it would be possible to correct for the different composition of treatment and control groups by using a regression model to control for the effects of this difference in impairment in estimating the impacts of channeling. Such a regression procedure was used to estimate the preliminary impact findings. However, regression alone may fail to account adequately for the effects of differential attrition for treatments and controls, for two reasons. First, the characteristics of the sample members who were lost due to attrition may be different in unknown ways from those who remain. Second, even if it were known how those who were lost due to attrition are different from those who remain, we seldom have the appropriate measures or know the appropriate functional form to control fully for the effect that these differences have on our outcome measures. In practice, the best we can do is to rely on some unverifiable statistical assumptions that enable us to use econometric procedures to control for the effects of attrition. The purpose of these statistical techniques is to purge an apparent treatment effect of any preexisting differences between those who are included in the sample and those who are lost due to attrition. The models and procedures are outlined below.
IV. A JOINT MODEL FOR PROGRAM IMPACTS AND ATTRITION
The regression model used in the preliminary analysis report (Kemper et al., 1984) to estimate channeling's impacts can be described as follows. Let Y1 be the outcome of interest, such as number of hospital days or number of nursing home days. Random assignment to treatment and control groups took place so that in theory these groups are equivalent on observed and unobserved characteristics.4 Define TB = 1 if the sample member belongs to the treatment group in the basic case management model, and TB = 0 if he or she does not. Similarly, define TF = 1 if the sample member belongs to the treatment group in the financial control model, and TF = 0 otherwise. Finally, define a set of auxiliary control variables (X1) such as site, sex, race, income, and impairment in functioning. As explained in Kemper et al. (1984), these variables are included in the outcome equation to control for preexisting differences between sample members on characteristics that determine jointly with channeling the value of the outcome. The model is then5
| (1) | Y1 | = | aBTB + aFTF + X1b1 + u1 |
| = | Zb + u1, |
where aB and aF are the estimates of the impact of channeling on the outcome, Y1, for the basic and financial control models, respectively; b1 is a vector of coefficients on the auxiliary variables; and u1 is the disturbance term. To facilitate the exposition below this equation is collapsed and expressed in terms of Z and b, where Z is a vector that contains variables TB, TF, and X1, and b is the true, unobserved value of the regression parameters (aB, aF, and b1) in equation (1). In the absence of sample attrition, if the random assignment to treatment or control groups was performed correctly and the usual assumptions of least-squares regression are satisfied, then regression estimates of aB and aF are unbiased estimates of the impacts of channeling on outcome Y1 for the basic case management and the financial control models, respectively.
As noted above, however, we could not estimate this model on the full sample of early enrollees because attrition did occur. To the extent that the included auxiliary control variables account fully for the effect of any differences between responders and nonresponders on the outcome variable (Y1), the estimated coefficients in equation (1), including aB and aF, remain unbiased. However, if there are unmeasured characteristics that affect both the probability of attrition and the outcome of interest, the estimated coefficients in equation (1) will in general be biased.
The following exposition describes the mechanism by which this bias occurs. Suppose that the attrition process can be described by the equations:
| (2) | 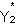 |
= | X2b2 + u2, and |
| (3) | Y2 | = | 1 if 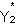 > 0 (in the analysis sample) > 0 (in the analysis sample) |
| Y2 | = | 0 if 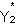 < 0 (lost from sample due to attrition). < 0 (lost from sample due to attrition). |
The dependent variable in equation (2) is an unobserved continuous variable, 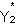 , representing the propensity to be available for and respond to the 6-month followup interview. The variable is not observed directly, but individuals with values exceeding a constant--without loss of generality assumed to be zero--are observed to respond (Y2 = 1), while those with values less than or equal to zero are nonresponders (Y2 = 0). Propensity to respond is assumed to be a function of observable characteristics, X2 (which includes treatment status and may include other variables also included in X1), as well as unobservable characteristics and circumstances, represented by the disturbance term u2, assumed to follow a standard normal distribution.
, representing the propensity to be available for and respond to the 6-month followup interview. The variable is not observed directly, but individuals with values exceeding a constant--without loss of generality assumed to be zero--are observed to respond (Y2 = 1), while those with values less than or equal to zero are nonresponders (Y2 = 0). Propensity to respond is assumed to be a function of observable characteristics, X2 (which includes treatment status and may include other variables also included in X1), as well as unobservable characteristics and circumstances, represented by the disturbance term u2, assumed to follow a standard normal distribution.
Bias arises in the estimates of aB and aF if the unobserved factors affecting attrition (u2) are correlated with the unobserved factors (u1) that affect the outcome measure (Y1). This can be seen by examining the genera]. expression for the vector of regression coefficients for equation (1), which we will refer to as 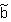 :
:
| (4) | 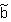 |
= | (Z'Z)-1Z'Y1, |
| = | b + (Z'Z)-1Z'u1. |
Without sample attrition, the expected value of the estimated regression coefficients is the true value of the parameters (b), because the last term in the expression above has an expected value of zero. With attrition, however,
| (5) | E(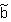 , given data available for analysis) , given data available for analysis) |
|
| = | b + E[(Z'Z)Z'u1, given Y2=1]. | |
| = | b + E[(Z'Z)-1Z'u1, given 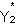 > 0] > 0] |
|
| = | b + E[(Z'Z)-1Z'u1, given u2 > -X2b2] | |
| = | b + (Z'Z)-1Z' E[u1, given u2 > -X2b2]. | |
If u1 and u2 are correlated (i.e., if there are unobserved factors that affect both Y1 and the probability of attrition), the final expected value of the expression in square brackets will not be zero, and therefore the expected value of the regression estimates of the parameters of equation (1), including the expected value of the estimates of aB and aF, will not be equal to the true values of these parameters. Thus, the estimates are biased by sample attrition, and the size and direction of the bias are unknown.6
The nature of this bias and a procedure for correcting it were explicated by Heckman (1976, 1979). Heckman showed that the bias due to sample attrition is analogous to the bias due to omitting an important explanatory variable. That is, we have
| (6) | E(Y1, given 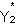 > 0) > 0) |
= | 1 if 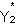 > 0 (in the analysis sample) > 0 (in the analysis sample) |
| = | Zb + E(u1, given u2 > -X2b2). |
As noted above, without sample attrition, the expected value of u1 is typically assumed to be zero, so estimates of b will be unbiased. However, when sample attrition exists, the regression can be estimated only on those sample members with complete data, so unbiasedness of the resulting estimates requires that the expected value of u1, conditional upon the observations available for analysis, be equal to zero. If u1 and u2 are correlated, however, this conditional expectation of u1 is not zero but is a function of u2 and X2. Inn this case, if Y1 is regressed on Z, and there is correlation between the variables in Z and those in X2, regression estimates of b will be biased because an "omitted" term (the nonzero conditional expected value of u1) is correlated with the regressors Z. The estimated coefficients on the variables in Z, including those on treatment status, will reflect not only the effect of Z on Y1, but also the relationship between Z and the conditional expectation of u1.
In this evaluation there is reason to believe that attrition can lead to bias in estimates of channeling impacts because those conditions that lead to bias may well be present. For example, suppose that the sample members who are the most impaired are least likely to respond and also likely to have systematically higher (or lower) values of Y1 (e.g., hospital days). Since the baseline control variables do not fully reflect impairment levels at the time of followup, u1 and u2 will be correlated. Furthermore, the variables Z and X2 that affect the outcome and the likelihood of attrition, respectively, are likely to be highly correlated (e.g., both the outcome and attrition probability may be affected by treatment/control status). Thus, there is a strong possibility that the two conditions that together produce biased estimates of regression parameters may be present and,' therefore, that estimates of channeling impacts will be biased by attrition.
Fortunately, with an additional assumption, a statistical correction for attrition bias is possible. Heckman showed that although the second term in the right-hand side of equation (6) is unobserved, the term has a relatively simple form if u1 and u2 are assumed to have a bivariate normal distribution, and this term can be estimated. Heckman shows that
| (7) | E(u1, given u2 > -X2b2) | = |  12 12 |
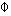 (X2b2/ (X2b2/ 2) 2) |
|
|
|
|||
 2 2 |
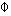 (X2b2/ (X2b2/ 2) 2) |
|||
| = |  12/ 12/ 2)M 2)M |
|||
where  12 is the covariance of u1 and u2,
12 is the covariance of u1 and u2,  2 is the standard deviation of u2, b2 is the vector of the estimated coefficients from the attrition equation,
2 is the standard deviation of u2, b2 is the vector of the estimated coefficients from the attrition equation, 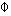 (X2b2/
(X2b2/ 2) is the standard normal density function evaluated at X2b2/
2) is the standard normal density function evaluated at X2b2/ 2, and
2, and 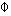 (X2b2/
(X2b2/ 2) is the standard normal distribution function evaluated at the same point. If the parameters b2 of the attrition equation were known, the term M could be constructed for each sample member and used as an additional variable in the regression model. Inclusion of this variable in this regression eliminates it from the error term and therefore eliminates the correlation between Z and the error term in equation (6), thereby eliminating the (asymptotic) attrition bias in estimates of b. The regression coefficient obtained on this M term is an estimate of
2) is the standard normal distribution function evaluated at the same point. If the parameters b2 of the attrition equation were known, the term M could be constructed for each sample member and used as an additional variable in the regression model. Inclusion of this variable in this regression eliminates it from the error term and therefore eliminates the correlation between Z and the error term in equation (6), thereby eliminating the (asymptotic) attrition bias in estimates of b. The regression coefficient obtained on this M term is an estimate of  12/
12/ 2), the (normalized) covariance between u1 and u2.
2), the (normalized) covariance between u1 and u2.
The parameters b2 are not known, but can be readily estimated. Thus, the procedure developed 'by Heckman and used in this report to eliminate attrition bias can be described as follows:
- Using all observations, estimate the parameters of the attrition model given in equations (2) and (3) using maximum likelihood probit.7
- From the estimated probit coefficients (b2) and the data on X2, form the correction term (M) for the observations which have valid data for the outcome regression--this excludes those lost due to attrition--and estimate equation (8) by least squares:8
| (8) | Y1 | = | aBTB + aFTF + X1b1 + cM + 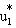 |
where this equation is simply equation (6) with the expression in equation (7) substituted for the nonzero conditional expectation of the disturbance term (u1), and 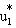 is the new disturbance term. The statistical significance of c, the coefficient on M, is an indication of whether there are unobserved factors affecting both attrition and Y1, a necessary condition for the estimates of aB and aF to be biased.
is the new disturbance term. The statistical significance of c, the coefficient on M, is an indication of whether there are unobserved factors affecting both attrition and Y1, a necessary condition for the estimates of aB and aF to be biased.
In the discussion of results in the next section, we assess the extent of attrition bias in estimates of channeling impacts by comparing the regression estimates of aB and aF obtained when potential attrition bias is not controlled for (i.e., from estimating equation (1)) to the impact estimates obtained when this potential bias is controlled for (by estimating equation (8)). In interpreting these results, it is useful to bear in mind the determinants of the bias in a particular coefficient. Inserting the expression in equation (7) into equation (4), the bias in the uncorrected estimates of aB , aF, and b1 is shown to be
| (9) | bias 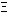 E( E( 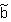 )-b )-b |
= | ( 12/ 12/ 2) (Z'Z)-1Z'M 2) (Z'Z)-1Z'M |
| = | ( 12/ 12/ 2) PZ,M, 2) PZ,M, |
where the term PZ,M is a vector of auxiliary regression coefficients obtained from regressing the constructed M term on the other variables (Z's) in equation (8).9 Thus, the bias in any particular regression coefficient (e.g., aB from the outcome equation) is equal to the covariance between u1 and u2 (normalized by  2), multiplied by the coefficient on this same variable (e.g., TB) from a second, auxiliary regression of the constructed M variable on all of the Z variables.
2), multiplied by the coefficient on this same variable (e.g., TB) from a second, auxiliary regression of the constructed M variable on all of the Z variables.
The usefulness of this expression is best demonstrated by elaborating on our previous example. Suppose that we are interested in estimating the impacts of channeling on the number of hospital days (using the followup sample). Also, suppose that those who are most impaired at the time of the followup are less likely to be available for analysis than are less impaired sample members and that the effects of this impairment on hospital days is imperfectly controlled for with the baseline control variables. Since the most impaired individuals are most likely to be in a hospital and least likely to be in the analysis sample, the covariance between u1 and u2 ( 12) will be negative. Furthermore, since treatment group members are more likely to be available for analysis than control group members, it can be shown that the auxiliary regression coefficient of treatment status contained in PZ,M is expected to be negative.10 Thus, we would expect the attrition bias in the estimate of aB to be positive. That is, the estimated impact will be a larger number than it should be. Thus, we could find an estimated impact of zero when in fact the impact was negative, implying a reduction in hospital days due to channeling. This analytic assessment of the direction of bias is consistent with the heuristic argument that the sample members most likely to be lost to analysis are control group members with relatively large numbers of hospital days, and if these cases were appropriately represented in the analysis sample, the treatment/control difference would have been a larger negative number. Based on this reasoning, the following reference table can be used to draw inferences about the expected direction of the bias (if any) due to attrition in estimates of channeling impacts:
12) will be negative. Furthermore, since treatment group members are more likely to be available for analysis than control group members, it can be shown that the auxiliary regression coefficient of treatment status contained in PZ,M is expected to be negative.10 Thus, we would expect the attrition bias in the estimate of aB to be positive. That is, the estimated impact will be a larger number than it should be. Thus, we could find an estimated impact of zero when in fact the impact was negative, implying a reduction in hospital days due to channeling. This analytic assessment of the direction of bias is consistent with the heuristic argument that the sample members most likely to be lost to analysis are control group members with relatively large numbers of hospital days, and if these cases were appropriately represented in the analysis sample, the treatment/control difference would have been a larger negative number. Based on this reasoning, the following reference table can be used to draw inferences about the expected direction of the bias (if any) due to attrition in estimates of channeling impacts:
Expected Relationship Between Y1 and the Likelihood That Sample Member is Available For Analysis ( 12) 12) |
Expected Bias1 in Estimated Impacts | Interpretation |
| 0 | 0 | Impact estimates unbiased |
| + | - | Impacts understated if channeling is predicted to increase Y (aB , aF positive); impacts overstated if channeling is predicted to decrease Y1 (aB , aF negative)2 |
| - | + | Impacts overstated if channeling is predicted to increase Y1 (aB , aF positive); impacts understated if channeling is predicted to decrease Y1 (aB , aF negative)2 |
|
||
Using this table for our example, we expect  12 to be negative because those who are most impaired are likely to have more hospital days, but are less likely to respond. Thus, the expected bias in the impact estimate is positive, and since channeling is predicted to reduce hospital days, the estimated reduction in hospital days will be understated if attrition bias is not corrected for.
12 to be negative because those who are most impaired are likely to have more hospital days, but are less likely to respond. Thus, the expected bias in the impact estimate is positive, and since channeling is predicted to reduce hospital days, the estimated reduction in hospital days will be understated if attrition bias is not corrected for.
V. EMPIRICAL RESULTS
As noted above, two separate attrition analyses are required: one for outcomes relying on the known status sample and one for outcomes using the followup sample. These samples differ in that, for those who were known to be deceased or in a nursing home at the point six months after randomization, the values of some of the outcome measures were known by definition. Outcome measures based on the known status sample and used in this analysis include where the sample member was living six months after randomization (in the community, in a nursing home, or in a hospital); whether they were deceased; and whether they received formal in-home care, the total hours of such care received, whether they received informal in-home care from nonhousehold members, and how many hours of such care they received during the week six months after randomization. The outcome measures based on the followup sample that were used to examine attrition bias in this report include whether the sample member received comprehensive case management during the preceding 6-month period, the number of hospital days and number of nursing home days during this period, the number of unmet needs the sample member reported, and the number of activities of daily living on which the sample members were impaired.
We investigate (separately for the two samples) the determinants of attrition by estimating probit models of whether the sample member was included in the analysis sample as a function of the following characteristics, obtained from the screening interview available for all sample members:
- Treatment/Control status
- Site
- ADL impairments
- Incontinence
- Monthly Income
- Living Arrangement
- Insurance Coverage
- Sex
- Age
- Ethnicity
- Number of unmet needs
- Whether a proxy was used to complete the screen
- Whether a sample member was in a hospital or nursing home at the screen
The results are reported in Table 2. The model appeared, based on the large and statistically significant chi-square goodness of fit statistic, to predict the probability of remaining in the sample reasonably well, for both of the samples considered. For the known status sample, we conclude, on the basis of the statistical significance (at the 95 percent confidence level) of the coefficients, that
- treatment group members are substantially more likely to be available for the analysis than controls
- sample members in some sites, especially Miami and Middlesex County, are less likely than those in other sites to be available for analysis
- those living with spouse or with children are significantly more likely to be available for analysis than those who live with other relatives, friends, or unrelated persons
- females are more likely to be available for analysis than males
- whites are less likely to be available for analysis than blacks or Hispanics
- those in hospitals or nursing homes at the time of the screen are less likely to be available for analysis than those who were not.
For the followup sample the results are similar, with the following exceptions:
- those impaired on eating are more likely to be lost from the sample
- those living with spouse or spouse and children are more likely to remain in the sample than are those with any other living arrangement
- both blacks and whites are significantly (and equally) less likely than Hispanics to remain in the sample
- sample members for whom proxy reports were used at the screen are less likely to remain in the sample than are those for whom self-reports were used
| TABLE 2. Probit Coefficients for Being in the Known Status Sample or the Followup Sample | ||||||
| Screen Variable | Known Status | Followup | ||||
| Coefficient | t-statistic | Impact on Probabilitya | Coefficient | t-statistic | Impact on Probabilitya | |
| Intercept | 1.152 | (3.52) | -- | 1.208 | (4.10) | -- |
| Research Status (1=treatment, 0=control) | .417** | (8.60) | 0.115 | .238** | (5.50) | 0.089 |
| Site | ||||||
| Basic Case Management | ||||||
| Baltimore | -.221 | (-1.71) | -0.061 | -.120 | (-1.04) | -0.045 |
| Eastern Kentucky | .157 | (1.09) | 0.043 | .125 | (0.99) | 0.047 |
| Houston | .017 | (0.13) | 0.005 | .030 | (0.26) | 0.011 |
| Middlesex County | -.287* | (-2.32) | -0.079 | -.279* | (-251) | -0.104 |
| Southern Maine | -.036 | (0.27) | -0.010 | -.039 | (-0.34) | -0.015 |
| Financial Control | ||||||
| Cleveland | .026 | (0.18) | 0.007 | -.101 | (-0.82) | -0.038 |
| Greater Lynn | -.049 | (-0.39) | -0.013 | .035 | (0.30) | 0.013 |
| Miami | -.399** | (-3.18) | -0.110 | -.242* | (-2.13) | -0.090 |
| Philadelphia | -.015 | (-0.12) | -0.004 | .054 | (0.48) | 0.020 |
| (Rensselaer County) | ||||||
| Impairment of Ability to Perform Activities of Daily Living (ADL)b (1=impaired, 0=not impaired) | ||||||
| Eating | -.084 | (-1.32) | -0.023 | -.146** | (-2.59) | -0.054 |
| Transfer | .112 | (1.63) | 0.031 | -.025 | (-0.41) | -0.009 |
| Toileting | -.076 | (-1.13) | -0.021 | -.084 | (-1.39) | -0.031 |
| Dressing | -.002 | (-0.03) | -0.001 | .059 | (1.03) | 0.022 |
| Bathing | -.042 | (-0.47) | -0.012 | -.113 | (-1.43) | -0.042 |
| Incontinenceb | .051 | (0.99) | 0.014 | -0.71 | (-1.55) | -0.026 |
| Monthly Income (dollars) | ||||||
| Less than 500 | .154 | (1.42) | 0.043 | .062 | (0.62) | 0.023 |
| 500-1000 | .059 | (0.58) | 0.016 | -.007 | (-0.07) | -0.003 |
| (Greater than 1000) | ||||||
| Usual Living Arrangement | ||||||
| Alone | .114 | (1.40) | 0.032 | .049 | (0.66) | 0.018 |
| With spouse or spouse and children | .181* | (2.04) | 0.050 | .161* | (2.01) | 0.060 |
| With child (no spouse) | .199* | (2.18) | 0.055 | .024 | (0.30) | 0.009 |
| (With other relatives or friends) | ||||||
| Insuranceb | ||||||
| Medicare, no Medicaid | .011 | (0.05) | 0.003 | .031 | (0.16) | 0.012 |
| Medicaid | .032 | (0.14) | 0.009 | .042 | (0.21) | 0.016 |
| Sex (1=male, 0=female) | -.113* | (-1.99) | -0.031 | -.290** | (-5.71) | -0.108 |
| Age | ||||||
| Less than 75 years | -.031 | (-0.45) | -0.009 | .053 | (0.88) | 0.020 |
| 75-79 | .010 | (0.14) | 0.003 | .046 | (0.73) | 0.017 |
| 80-84 | -.095 | (-1.42) | -0.026 | -.083 | (-1.40) | -0.031 |
| (Greater than 84) | ||||||
| Ethnic Background | ||||||
| Black | -.239 | (-1.57) | -0.066 | -.492** | (-3.69) | -0.183 |
| White | -.466** | (-3.23) | -0.128 | -.553** | (-4.33) | -0.206 |
| (Hispanic) | ||||||
| Number of Unmet Needsb (ranging from 0 to 5) | -.036 | (-1.52) | -0.010 | -.037 | (-1.75) | -0.014 |
| Proxy Use (1=all or partial proxy at screen, 0=self-report) | -.065 | (-1.09) | -0.018 | -.117* | (-2.19) | -0.044 |
| Institutionalized at screen (1=yes, 0=no) | -.168** | (-2.82) | -0.046 | -.222** | (-4.15) | -0.083 |
| Number of cases in the cohort used for analysisc | 3,799 | 3,799 | ||||
| Number of cases in the analysis | 3,062 (80.6%) | 2,477 (64.4%) | ||||
| Chi-squared | 179.25 | 201.32 | ||||
| Degrees of Freedom | 37 | 37 | ||||
NOTE: For categorical variables, omitted reference categories are designated in parentheses.
*Statistically significant at the 95 percent confidence level for a two-tailed test. **Statistically significant at the 99 percent confidence level for a two-tailed test. |
||||||
Impairment on eating is the most severe impairment of activities of daily living and its large effect on attrition from the followup sample (but not from the known status sample) may be partially due to the higher likelihood of death for those who were extremely impaired at the screen. Similarly, it could be suggested that proxy use at screen is an indicator of frailty--the sample member is too sick to respond--which could explain its important role in predicting attrition from the followup sample. The other differences between the results for the two samples are harder to interpret, which may be because the factors leading to death are different from those leading to interview nonresponse. The probit coefficients reflect the combined influences of both factors.11
The estimates in Table 2 were used to form the correction term (M) to estimate the impact model given in equation (8) that corrects for attrition. The set of auxiliary control variables (X1) used here is a subset of those used in the preliminary impact analysis12
- site
- ADL impairments (extremely severe through mild)
- income categories
- living arrangement
- insurance
- sex
- age categories
- ethnic group (black, white, Hispanic)
- proxy use
- number of unmet needs at baseline
- global life satisfaction index
- number of nursing home days and number of hospital days during two months prior to randomization
- hours of formal and informal care during baseline reference week
The unadjusted and adjusted impact estimates (the difference between treatments and controls) for the basic case management model and the financial control model are presented in Table 3. The last column in Table 3 gives the number of observations used in estimating the impacts on the outcomes. At the most, 5 percent of the observations were omitted due to missing values on the dependent variable. The coefficients on the correction term (M) are also given, in the fifth column. None of the coefficients in this column is significant, indicating that net of the included auxiliary variables and treatment status the added term does not have a significant effect on the outcomes considered. Since this coefficient is an estimate of the (normalized) covariance of the two disturbance terms, and a nonzero covariance is a necessary condition for attrition bias, this suggests that there is no bias in the impact estimates.
An alternative and perhaps more reliable indicator of the extent of bias in the estimated impacts is the difference between the impact estimates obtained with and without the selection bias correction term (M). When adjusting for attrition bias we find very minor changes in the impact estimates for most of the outcome measures. However, for three outcomes we find a considerable change of the magnitude of the impact estimate after correction. In the followup sample, after adjustment for attrition bias, the estimated impact of channeling on the number of nursing home days falls by a little more than a day for both models, and the estimated reduction in number of unmet needs rises by 0.1. Both of these changes represent large proportionate changes in the impact estimates. For the significance levels reported here, there is no change in the statistical significance of the estimates, but in both instances that would not be so for one of the models if a 90 percent confidence level were used. For the known status sample, after the effects of attrition are controlled for, we observe considerably larger reductions in the amount of informal in-home care provided by caregivers who live outside the home. This is especially noteworthy for the basic sites, where the estimate doubles in magnitude and goes from being statistically insignificant to being statistically significant. There are two other instances (percent receiving formal in-home care and percent hospitalized) for which the estimate changes very little, but due to the increase in standard errors, the statistical significance of the estimate drops. Since the impact estimates do not change, we conclude that the estimated impacts of channeling on percent receiving formal in-home care and percent hospitalized are not affected by attrition, and that the original impact estimates are not biased by effects of attrition.
Explaining the results is difficult. For example, if control group members who are most impaired and in need of care were less likely to respond than comparable treatment group members, then the treatment/control differences in factors related to impairment would tend to be overestimated. This could explain the larger negative impact estimates after controlling for the effects of attrition on unmet needs and hours of informal care. However, the impact on the number of nursing home days changed in the opposite direction. Thus, we have no readily apparent explanation that is consistent with all of the results.
| TABLE 3. Estimates of Impacts of Channeling With and Without Adjustment for Attrition | |||||||
| Outcome | Case Management Model | Financial Control Model | M-terma | 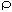 b b |
Sample Size | ||
| Unadjusted | Adjusted | Unadjusted | Adjusted | ||||
| FOLLOWUP SAMPLE | |||||||
| Percent Receiving Comprehensive Case Management During First 6-Month Period | 48.59** (19.54) | 48.10** (16.80) | 50.45** (18.45) | 50.0** (16.94) | -0.04 (-0.34) | -0.089 | 2,346 |
| Number of Hospital Days in Last Six Months | -2.28 (-1.50) | -2.48 (-1.42) | 1.24 (0.77) | 1.06 (0.59) | -1.49 (-0.22) | -0.059 | 2,365 |
| Number of Nursing Home Days in Last Six Months | -1.81 (-0.88) | -0.54 (-0.23) | -3.90 (-1.78) | -2.79 (-1.15) | 9.41 (1.04) | 0.271 | 2,365 |
| Number of Unmet Needs Six Months After Randomization | -0.15 (-1.32) | -0.25 (-1.86) | -0.38** (-3.16) | -0.47** (-3.47) | -0.71 (-1.41) | -0.370 | 2,293 |
| ADL Scorec | -0.01 (-0.12) | 0.02 (0.25) | 0.05 (0.59) | 0.08 (0.84) | 0.24 (0.69) | 0.182 | 2,318 |
| KNOWN STATUS SAMPLE | |||||||
| Percent Living Six Months After Randomization in: | |||||||
| Community | 0.27 (0.12) | 0.07 (0.02) | 0.81 (0.32) | 0.61 (0.17) | -0.01 (-0.07) | -0.027 | 3,062 |
| Hospital | -2.77* (-2.16) | -2.42 (-1.24) | -0.98 (-0.72) | -0.64 (-0.33) | 0.02 (0.24) | 0.087 | 3,062 |
| Nursing home | 0.84 (0.58) | 0.81 (0.37) | -0.11 (-0.07) | -0.14 (-0.06) | -0.00 (-0.02) | -0.007 | 3,062 |
| Percent Deceased Six Months After Randomization | 1.66 (0.89) | 1.54 (0.54) | 0.29 (0.14) | 0.17 (0.06) | -0.01 (-0.05) | -0.020 | 3,062 |
| Percent Receiving Formal In-Home Cared | 6.68** (2.58) | 6.51 (1.65) | 12.93** (4.68) | 12.77** (3.20) | -0.01 (-0.06) | -0.021 | 2,940 |
| Percent Receiving Informal In-Home Cared | -3.82 (-1.48) | -2.72 (-0.69) | -1.73 (-0.63) | -0.66 (-0.17) | 0.07 (0.37) | 0.138 | 2,925 |
| Total Hours of Formal In-Home Cared | 0.03 (0.04) | 0.11 (0.09) | 4.15** (4.80) | 4.22** (3.39) | 0.46 (0.08) | 0.031 | 2,940 |
| Hours of Informal In-Home Care From Caregivers who Live Outside the Homed | -1.58 (-1.59) | -3.34* (-2.16) | -0.80 (-0.75 | -2.50 (-1.59) | -10.49 (-1.50) | -0.536 | 2,925 |
NOTE: T-statistics are in parentheses.
*Statistically Significant at the 95 percent confidence level for a two-tailed test. **Statistically Significant at the 99 percent confidence level for a two-tailed test. |
|||||||
VI. CONCLUSION
In conclusion, we note that no global patterns of attrition bias emerge; the evidence for the existence of bias and the estimated magnitude and direction of the bias depend clearly on the outcome considered. For both the basic case managment model and the financial control model, we found that controlling for the effects of attrition led to very small changes in estimates of channeling's impacts on most of the outcome measures examined, but to fairly large changes in estimated impacts on number of nursing home days, number of unmet needs, and hours of informal in-home care provided by caregivers who live outside the home. However, even for these variables the estimate of the normalized covariance between the disturbance terms is not statistically different from zero, a condition which is necessary for bias to exist. Thus, although attrition bias does not appear to have led to fundamental errors in inferences about the existence and direction of effects of channeling in the preliminary impact analysis (at least for the set of key outcomes examined here), the results indicate that attrition is clearly a factor to take into consideration in future impact analyses. As the 12- and 18-month followup interviews are administered, attrition will increase, exacerbating the potential importance of attrition bias.
It is important to note some limitations of the results presented here, some of which may be eliminated in future analyses of the effects of attrition on impacts. First, in the attrition model, attrition due to death is not distinguished from attrition due to interview nonresponse which makes the probit coefficients used in the correction term difficult to interpret. Further investigation is necessary to determine whether, and if so, how, the specification of the attrition model (a single equation versus separate equations for death and nonresponse) affects the estimates of bias in our impact estimates. Second, it is important to allow the parameters for the attrition equation to differ by model. Thus, identical sample members in the two models may have very different correction terms if the data indicate that this is warranted. Separate models will be estimated in subsequent analyses of attrition. Third, we have relied on the assumption of a bivariate normal distribution of the disturbance terms of the impact equation and the attrition equation, which is not technically correct for categorical outcome variables. Although it has been shown in the current statistical literature that the bivariate normality assumption may not be innocuous, no tractable methods have been proposed yet that require less objectional assumptions. Fourth, the impact model considered here is a limited version of the impact models used in the preliminary findings report; many more auxiliary variables are included in the latter. For the final report we will use identical models. Fifth, possible attrition bias in the impacts for subgroups are not considered in the present attrition analysis. If we have important subgroup findings in the final analysis, we will consider the need to examine the effects of attrition on the subgroup results. Finally, other researchers have suggested that the two-step correction procedure used here tends to overcorrect the impact estimates (Griliches, Hall, and Hausman, 1978), as compared to a maximum likelihood procedure. Unfortunately, maximumum likelihood estimation is considerably more expensive and complicated to implement.
For the final report we will attempt to improve the specification of the attrition model. We will also have additional data on outcome variables from other sources (death records, Medicare, and Medicaid records) that will allow us to limit the extent of loss of observations from the analysis due to attrition, and to evaluate how well the procedures employed to correct for attrition bias actually perform.
NOTES
-
"Attrition" in this report is defined as the loss of sample members for analysis purposes, i.e., as the lack of followup data on required outcome measures. The term attrition does not refer to treatment group members who do not participate in channeling (i.e., those who decline, those determined at baseline to be ineligible, and those terminated from the demonstration).
-
Followup interviews were only attempted for sample members who complete baselines; thus, nonresponse to the baseline implies nonresponse at the followup as well.
-
Baseline assessment interviews were administered by channeling project staff to members of the treatment group and by research interviewers for the control group. In addition, research interviewers attempted to complete a baseline interview with those treatment group members who failed to complete the channeling-administered baseline interview. For the full research sample, this additional attempt improved the treatment group response rate by 4.1 percentage points in the basic sites, and by 2.0 percentage points in the financial control sites. The response rates reported include all completed baselines, whether administered by channeling staff or research interviewers.
-
See Brown and Harrigan (1983) for evidence that the full treatment and control groups are very similar on a wide variety of screen characteristics.
-
Minor changes in notation from that used in the preliminary findings report (Kemper et al., 1984) are made to clarify the presentation.
-
Throughout this discussion, X1 is treated as being fixed. The same results can be obtained for random X1 variables by making all expectations conditional upon X1.
-
The probit model (Finney, 1964) is used to predict a binary response (Y2 = 1 or 0) as a function of explanatory variables X2:
Prob(Y2 = 1) = 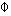 (X2b2),
(X2b2),where
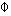 is the cumulative distribution function of the normal standard distribution.
is the cumulative distribution function of the normal standard distribution. -
The standard errors from the least squares regression with the correction term are not correct due to heteroskedasticity introduced by the M-term. We have corrected the standard errors using methods based on Heckman (1979) and Greene (1981).
-
It can easily be shown that evaluating the expression in equation (9) yields estimates of the bias that are identical to those obtained by computing the difference between the coefficients obtained from the adjusted and unadjusted regressions.
-
The auxiliary regression coefficient on a variable in Z obtained from the regression of M on Z will tend to have a sign which is opposite to the expected sign of the correlation between that variable and the likelihood that the sample member is available for analysis. Since treatment group members are more likely to respond, the latter correlation will be positive, and the auxiliary regression coefficient will be negative.
-
As pointed out in Chapter III, there are several ways in which sample members can be lost to the analysis, including interview refusal, death of the sample member, moving, or just failure to locate the sample member. For the two most prevalent reasons for missing data--sample member death or refusal--a single equation may not model both processes adequately. In theory, it is possible to use separate equations for death and nonresponse, to form two different M-terms and include these in the outcome equation. We have not chosen this procedure since the analysis would be complicated considerably (especially the computation of standard errors of the estimates). We relied instead on a reduced form equation to represent attrition due both to death and to nonresponse. In Appendix A, we estimate a multinomial logit model in which the followup sample members could fall into one of three possible response categories: death, nonresponse, and completed 6-month followup interview. However, it is important to note that the method of correction for attrition bias that uses a single attrition equation is still correct, since all that is required to account for the bias due to attrition is the inclusion of a measure of the total effects of observed variables on the probability of attrition.
-
This change was made to keep computational costs down and should have no effect on the basic conclusions concerning the presence or absence of selection bias. See Appendix B for a comparison of the results presented in the preliminary findings report (Kemper et al., 1984) to the results obtained from the regressions used here. Complete descriptions of the control variables are also given in Kemper et. al (1984).
APPENDIX A. A MULTINOMIAL LOGIT MODEL OF RESPONSE, DEATH, AND NONRESPONSE
The probit coefficients for the probability of being included in the followup sample, as presented in Table 2, reflect the combined influences of factors leading to death-and nonresponse. It is emphasized again that the method used to correct for attrition bias does not require separate equations for attrition due to death and nonresponse. However, since the relationship between sample member characteristics and death attrition may differ considerably from the relationship between these characteristics and interview refusal, the coefficients of the probit model are not very informative about the determinants of attrition. Such information may be gained from a model in which the followup sample members could fall into one of three possible response categories: death, and for those who survive, interview nonresponse and completed 6-month followup interview. Unfortunately, a trinomial probit is computationally difficult to implement, so we have used a close alternative to the probit model, namely a multinomial logit model. Under this model the probabilities of death, interview nonresponse, and followup completion are, respectively:
Prob(death) =
/ (
+
+ 1)
Prob(interview nonresponse) =
/ (
+
+ 1)
Prob(completed 6-month followup interview) = 1 / (
+
+ 1).
In this model, we obtain two sets of coefficients, bd and bn, from which the predicted probabilities of death, interview nonresponse, and completed 6-month followup interview can be derived. The results are presented in Table A-1. We find that the following factors are statistically significant predictors of attrition from the analysis sample due to death: being impaired on eating and transfer, incontinence, being male, being black or white (as opposed to Hispanic), and being institutionalized at the screen. Except for the sex and ethnic group variables, these factors can be interpreted as indicators of severe frailty due to medical conditions that precede death.
A high probability of interview nonresponse in the followup sample is associated with being in the control group; being from the Middlesex County or the Miami sites; living with children or alone, rather than living with a spouse; being black or white, rather than Hispanic; having a high number of unmet needs; and the use of a proxy at the screen. An explanation of why control group members are more likely to refuse to be interviewed is that they were disappointed about the fact that they would not receive channeling benefits. It is difficult at this point to give a. good interpretation of the effects of race and unmet needs. Proxy use at the screen seems to be an indication of proxy respondents not wanting to be bothered by an interview.
Likelihood ratio tests confirm what is apparent from these two sets of estimates, that is, that the relationship between sample member characteristics and attrition depends on the type of attrition. Future analyses of attrition bias will investigate whether there are efficiency gains to be achieved by incorporating separate correction terms for nonresponse and death in the regression models used to estimate channeling's impacts.
| TABLE A-1. Multinomial Logit Coefficients for Response Status at Six-Month Followup(t-statistics in parentheses) | ||||
| Screen Variable | Death vs. Complete | Nonresponse vs. Complete | ||
| Intercept | -3.98 | (-5.78) | -1.90 | (-3.25) |
| Research Status (1=treatment, 0=control) | 0.03 | (0.26) | -0.68** | (-7.93) |
| Site (within model) | ||||
| Basic Case Management | ||||
| Baltimore | -0.10 | (-0.39) | 0.41 | (1.76) |
| Eastern Kentucky | 0.01 | (0.04) | -0.36 | (-1.36) |
| Houston | -0.44 | (-1.66) | 0.22 | (0.94) |
| Middlesex County | 0.29 | (1.19) | 0.61** | (2.73) |
| Southern Maine | 0.17 | (0.67) | -0.01 | (-0.02) |
| Financial Control | ||||
| Cleveland | -0.04 | (-0.15) | 0.33 | (1.34) |
| Greater Lynn | -0.07 | (-0.27) | -0.01 | (-0.04) |
| Miami | -0.16 | (-0.62) | 072** | (3.21) |
| Philadelphia | -0.32 | (-1.31) | 0.07 | (0.30) |
| Impairment of Ability to Perform Activities of Daily Living (ADL)a | ||||
| Eating | 0.38** | (3.27) | 0.08 | (0.73) |
| Transfer | 0.36* | (2.51) | -0.16 | (-1.30) |
| Toileting | 0.24 | (1.66) | 0.08 | (0.68) |
| Dressing | -0.14 | (-0.99) | -0.07 | (-0.65) |
| Bathing | 0.41 | (1.94) | 0.07 | (0.48) |
| Incontinencea | 0.33** | (3.06) | -0.03 | (-0.36) |
| Monthly Incomea | ||||
| <500 | 0.28 | (1.22) | -0.34 | (-1.77) |
| 500-1000 | 0.30 | (1.37) | -0.18 | (-1.02) |
| Living Arrangement | ||||
| With spouse | -0.20 | (-1.10) | -0.33* | (-2.11) |
| With children | 0.16 | (0.93) | -0.22 | (-1.39) |
| Alone | 0.04 | (0.26) | -0.19 | (-1.28) |
| Insurancea | ||||
| Medicare | -0.11 | (-0.24) | 0.02 | (0.04) |
| Medicaid | -0.12 | (-0.28) | -0.01 | (-0.03) |
| Sex (1=male, 0=female) | 0.82** | (7.36) | 0.21* | (2.05) |
| Age | ||||
| <75 | -0.05 | (-0.38) | -0.12 | (-0.98) |
| 75-79 | -0.12 | (-0.86) | -0.03 | (-0.27) |
| 80-84 | 0.19 | (1.47) | 0.11 | (0.90) |
| Ethnic Background | ||||
| Black | 1.08** | (3.18) | 0.59* | (2.16) |
| White | 0.85** | (2.59) | 0.94** | (3.62) |
| Number of Unmet Needsa (0-5) | 0.02 | (0.37) | 0.10** | (2.25) |
| Proxy Usea (1=all or partial proxy, 0=self report) | 0.19 | (1.46) | 0.19* | (1.80) |
| Institutionalized at screen (1=yes, 0=no) | 0.55** | (4.92) | 0.19 | (1.77) |
| Sample sizeb | 3799 | |||
| Chi-square statisticc | 359.81** | |||
| Degrees of Freedom | 74 | |||
NOTE: The logit model was estimated to distinguish sample members who completed the 6-month followup interview from those who had died and from those who were nonrespondents. Logit coefficients are interpretable as estimates of the impact of the corresponding variables on the log odds ratios (i.e., on the percent change in the relative odds) of death versus response (column 1) and nonresponse versus response (column 2). Coefficients were estimated by maximum likelihood. T-statistics are in parentheses.
*Statistically significant at the 95 percent confidence level for a two-tailed test. **Statistically significant at the 99 percent confidence level for a two-tailed test. |
||||
APPENDIX B. COMPARISON OF RESULTS TO THOSE PRESENTED IN CHANNELING EFFECTS FOR AN EARLY SAMPLE AT 6-MONTH FOLLOWUP
For two reasons the unadjusted impact estimates presented in this report differ from those in the preliminary impact analysis, which are presented in Kemper et al. (1984). First, to lessen the costs of the computation-intensive bias correction method, we have used a shorter list of explanatory variables in the unadjusted and adjusted impact regressions. As a consequence, the unadjusted impact estimates will differ from chose in Kemper et al. (1984). Second, we excluded from analyses those observations for whom no M-term could be constructed because of missing values on the screen variables used to construct the M-term. This exclusion causes our sample size to be slightly (about 1 percent) smaller than the sample size of the preliminary analysis.
The assessment of whether there is attrition bias in estimates of channeling impact should be unaffected by this difference in regressors, since variables that tended to be significant in the full outcome regressions in Kemper et al. (1984) were the ones that were retained. Furthermore, because of random assignment, these variables will tend to be relatively uncorrelated with treatment status; hence, omitting them is unlikely to yield different estimates of channeling impacts. Nonetheless, in order to verify that the results on attrition bias obtained from the model with the reduced set of regressors used in this report (Table 3) are comparable to results that would be obtained from the full regression model used throughout the preliminary analysis, we compare (Table B.1) the unadjusted results from Table 3 to the impact estimates that are presented in Kemper et al. (1984) for the same set of outcomes.
We observe that for none of the outcomes is there a difference in the statistical significance of the impact estimates. Moreover, the statistically significant impacts change relatively little in magnitude; only the small and statistically insignificant impacts exhibit changes of any magnitude. Since coefficients with small t-values are generally more sensitive to alternative model specifications than coefficients with a large t-value, these changes are not deemed important. We conclude from this comparison that the results obtained on attrition bias in this report are comparable to those that would be obtained for the fuller regression model, and that therefore the conclusions drawn here concerning attrition bias are applicable to the impact estimates presented in the preliminary analysis.
| TABLE B-1. Comparison of Impact Estimates in Preliminary Analysis Report to Unadjusted Impact Estimates Used in Attrition Analysis(t-statistics in parentheses) | ||||||
| Basic Model | Financial Control Model | Sample Sizesa | ||||
| Attrition Analysis | Preliminary Analysis Report | Attrition Analysis | Preliminary Analysis Report | Attrition Analysis | Preliminary Analysis Report | |
| FOLLOWUP SAMPLE | ||||||
| Percent Receiving Comprehensive Case Management During First 6-Month Period | 48.59** (19.54) | 49.11** (19.56) | 50.45** (18.45) | 51.4** (18.86) | 2,346 | 2,395 |
| Number of Hospital Days in Last Six Months | -2.28 (-1.50) | -2.43 (-1.59) | 1.24 (0.77) | 1.30 (0.79) | 2,365 | 2,391 |
| Number of Nursing Home Days in Last Six Months | -1.81 (-0.88) | -2.45 (-1.20) | -3.90 (-1.78) | -2.87 (-1.31) | 2,365 | 2,391 |
| Number of Unmet Needs Six Months After Randomization | -0.15 (-1.32) | -0.13 (-1.14) | -0.38** (-3.16) | -0.38** (-3.05) | 2,293 | 2,319 |
| ADL Scoreb | -0.01 (-0.12) | 0.00 (0.03) | 0.05 (0.59) | 0.08 (0.91) | 2,318 | 2,347 |
| KNOWN STATUS SAMPLE | ||||||
| Percent Living Six Months After Randomization in: | ||||||
| Community | 0.27 (0.12) | 0.99 (0.43) | 0.81 (0.32) | 1.62 (0.65) | 3,062 | 3,097 |
| Hospital | -2.77* (-2.16) | -2.84* (-2.19) | -0.98 (-0.72) | -0.84 (-0.60) | 3,062 | 3,097 |
| Nursing home | 0.84 (0.58) | -0.15 (-0.10) | -0.11 (-0.07) | 0.35 (0.22) | 3,062 | 3,097 |
| Percent Deceased Six Months After Randomization | 1.66 (0.89) | 2.00 (1.07) | 0.29 (0.14) | -1.13 (-0.56) | 3,062 | 3,097 |
| Percent Receiving Formal In-Home Care | 6.68** (2.58) | 7.20** (2.78) | 12.93** (4.68) | 13.60** (4.88) | 2,940 | 2,972 |
| Percent Receiving Informal In-Home Care | -3.82 (-1.48) | -2.60 (-1.01) | -1.73 (-0.63) | -0.20 (-0.08) | 2,925 | 2,958 |
| Total Hours of Formal In-Home Care From Visiting Providers | 0.03 (0.04) | 0.07 (0.08) | 4.15** (4.80) | 4.26** (4.86) | 2,940 | 2,972 |
| Hours of Informal In-Home Care From Caregivers Who Live Outside the Home | -1.58 (-1.59) | -1.55 (-1.54) | -0.80 (-0.75) | -0.42 (-0.38) | 2,925 | 2,958 |
*Significant at the 95 percent level for a two-tailed test. **Significant at the 99 percent level for a two-tailed test. |
||||||
CHANNELING EVALUATION REPORTS
Preliminary Reports
-
The Planning and Implementation of Channeling: Early Experiences of the National Long Term Care Demonstration. Raymond J. Baxter et al. April 15, 1983. [http://aspe.hhs.gov/daltcp/reports/implees.htm]
-
Channeling Effects for an Early Sample at 6-Month Followup. Peter Kemper et al. June 1984. [http://aspe.hhs.gov/daltcp/reports/6monthes.htm]
Technical Reports
-
Research Design of the National Long Term Care Demonstration. Peter Kemper et al. November 1982. [http://aspe.hhs.gov/daltcp/reports/designes.htm]
-
Informal Care to the Impaired Elderly: Report of the National Long Term Care Demonstration Survey of Informal Caregivers. Jon B. Christianson and Susan A. Stephens. June 6, 1984. [http://aspe.hhs.gov/daltcp/reports/impaires.htm]
Supplementary Reports
-
Differential Impacts Among Subgroups of Early Channeling Enrollees Six Months After Randomization. Thomas W. Grannemann, Randall S. Brown, and Shari Miller Dunstan. July, 1984. [http://aspe.hhs.gov/daltcp/reports/difimpes.htm]
-
The Effects of Sample Attrition on Estimates of Channeling Impacts for an Early Sample. Peter Mossel and Randall S. Brown. July 1984. [http://aspe.hhs.gov/daltcp/reports/earlyes.htm]
Reports are Available From: Mathematica Policy Research, Inc. P.O. Box 2393 Princeton, New Jersey 08540
REFERENCES
Brown, R. and M. Harrigan. "The Comparability of Treatment and Control Groups at Randomization." Mathematica Policy Resarch, Princeton, N.J., October 1983. [http://aspe.hhs.gov/daltcp/reports/compares.htm]
Catsiapis, G. and C. Robinson. "Sample Selection Bias with Multiple Selection Rules." Journal of Econometrics, Vol. 18, 1982, pp. 351-68.
Finney, D.J. Statistical Methods in Biological Assay. Second Edition, 1964. London: Griffin.
Greene, W.H. "Sample Selection Bias as a Specification Error: Comment." Econometrica, Vol. 49, 1981, pp. 795-98.
Griliches, Z., B.H. Hall, and J.A. Hausman. "Missing Data and Self-Selection in Large Panels." Annales de l'INSEE 30-31, 1978, pp. 137-76.
Heckman, J. "The Common Structure of Statistical Models of Truncation, Sample Selection, and Limited Dependent Variables, and a Simple Estimator for Such Models." Annals of Economic and Social Measurement, Volume 5, Fall 1976, pp. 475-492.
Heckman, J. "Sample Selection Bias as a Specification Error." Econometrica, Vol. 47, 1979, pp. 153-61.
Kemper, P. et al. "Channeling Effects for an Early Sample at 6-Month Followup." Channeling Evaluation Preliminary Report #2, June 1984. [http://aspe.hhs.gov/daltcp/reports/6monthes.htm]
